Number Theory

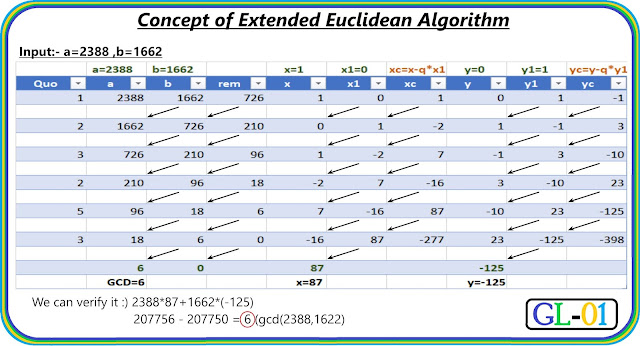
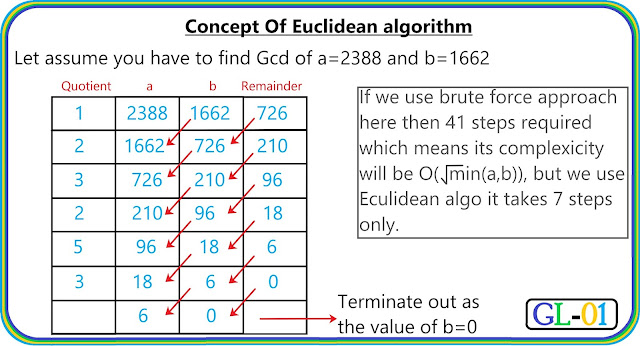
Hey, Guys in this part we are going to know about what is  Extended Euclidean Algorithm   and how we can  apply this concept in our programs. In our last blog we know about what is  Euclidean Algorithm  , now in this part we exlore more about extended Euclidean Algorithm. The extended Euclidean algorithm is an algorithm to compute integers   x   and   y   such that                                                        a.x + b.y = gcd(a,b)               , for  given   a   and   b . The existence of such integers is guaranteed by  Bézout's lemma   . Explanation (Recursive version) Let , gcd=gcd(a,b) & x,y be the co-efficient of a,b in x.a + y.b = gcd  equation.----(i) If we recall the Eculidean algorithm, we can see that the algorithm ends with b = 0  and a=gcd in such condition x should be 1 and y be 0 so, 1.a+ 0.0 = gcd . So starting coefficient of (x,y)=(1,0). Now we have to calculate futher coefficient for (b,a%b) , which also satisfy equation(i) ,  x1.b + y1.(a%b) = g

Hey, Guys in this part we are going to know about what is   Euclidean algorithm which is used   to find Gcd of two numbers  and how we can  apply this concept in our programs. BruteForce approach to find Gcd  If , we have to calculate the Gcd of two numbers a , b then the basic approach is to traverse form 1 to min(a,b) and then find max value of  iteration  variable which divide  both numbers. We have same approach in updated version also in which , we have to traverse only from 1 to Square root min(a,b).  But both of two  approach are Brute force approach and have complexicity of O(min(a,b)) and O(sqrt(min(a,b))) respectively. Let see code in C++ int   GCD ( int   a , int   b ) {    int   min_value = min ( a , b );    int   max_value = max ( a , b );    int   Gcd = 1 ;    if ( max_value % min_value == 0 ) {  Gcd = min_value ; }    else   {    for ( int   i = 1 ; i <= sqrt ( min_value )+ 1 ; i ++) { if ( a % i == 0  &&  b % i == 0 )   Gcd = i ;}   }     return   Gcd ; } T

Hey, Guys in this part we are going to know about what is  Binary Exponentiation and how we can  apply this concept in our programs. If you have to calculate    x 25  , first basic approach is  multiply  x  by itself 24 times. But if  x  is large enough (in millions), even just one multiplication is time consuming and also the complexicity  of this approach is O(n). Can we have better option, Yes here we introduce you a better algorithm known " Binary Exponentiation" , this algo does same work in the complexicity of O(log(n)). Let see how it works. Binary Exponentiation The key  idea of binary exponentiation is, that we split the work using the binary representation (multiple of 2). Multiple of 2 is optimal as numbers in computer systems are stored in base 2 and squares are a single instruction as it involves shifting bits right one position. The basic concept of this approach work as:-                    a b + c   = a b ⋅ a c   The complexity of this algorithm is  O ( log n