What is Extended Euclidean Algorithm

Hey, Guys in this part we are going to know about what is Extended Euclidean Algorithm  and how we can  apply this concept in our programs.

In our last blog we know about what is Euclidean Algorithm , now in this part we exlore more about extended Euclidean Algorithm.The extended Euclidean algorithm is an algorithm to compute integers $x$ and $y$ such that 

                                                      a.x + b.y = gcd(a,b)              ,for given $a$ and $b$.

The existence of such integers is guaranteed by Bézout's lemma .

Explanation

(Recursive version)

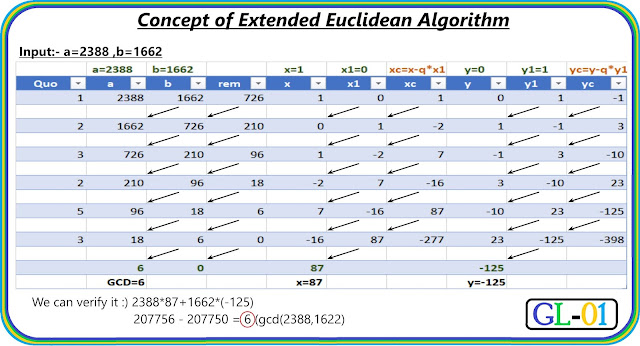
Let , gcd=gcd(a,b) & x,y be the co-efficient of a,b in x.a + y.b = gcd equation.----(i)

If we recall the Eculidean algorithm, we can see that the algorithm ends with b$=0$ and a=gcd in such condition x should be 1 and y be 0 so, 1.a+ 0.0 = gcd. So starting coefficient of (x,y)=(1,0).

Now we have to calculate futher coefficient for (b,a%b) , which also satisfy equation(i) , x1.b + y1.(a%b) = gcd---------(ii)

we can write (a%b) = remainder = a - quotient.b , 

put the value of (a%b) in equation (ii)

we get, x1.b + y1.(a - quotient.b)=gcd

            y1.a + (x1 - quotient).b = gcd which also equal to gcd =  a.x + b.y

By comparing coefficient we get the value of  x = y1  &  y = (x1 - quotient).

 Let see code in c++,

int gcd(int a, int b, int *x, int *y)

{

    if(a==0)

    {

        *x=0;

        *y=1;

        return b;

    }

    int x1, y1; 

    int g=gcd(b%a,a,&x1,&y1);

    *y=x1;

    *x=y1-(b/a)*x1;

     return g;

}

 

int main()

{

    int a,b;

    cin>>a>>b;

    int x, y;

    int g=gcd(a, b, &x, &y);

    cout<<x<<" X "<<a<<" + "<<y<<" X "<<b<<" = "<<g<<endl;

    return 0;

}

Iterative version

This approach is similar to recursive one but only diffrence, it avoids recursion, the code will run a little bit faster than the recursive one. 

Here we use one property only that : xc=x-quotient*x1   &  yc=x-quotient*y1 

Let see code in c++

int main()

{   

int a,b;

cin>>a>>b;// take input for finding gcd 

int x=1,y=0;

int x1=0,y1=1;

int xc,yc;

int rem,q; // variables to store remainder and quotient

while(b>0)

{

  rem=a%b;

  q=a/b;

  a=b;

  b=rem;

  xc=x-q*x1;

  yc=y-q*y1;

  x=x1;

  x1=xc;

  y=y1;

  y1=yc;

}

cout<<"X-> "<<x<<" y-> "<<y<<" Gcd-> "<<a<<endl;

 return 0;

}

Practice problem

GeeksForGeeks P1

OnlineJugde P1

OnlineJugde P2

OnlineJudge P3

May these Information will be useful for you, 

Have a Nice Day😀😀😀.