Hey, Guys in this part we are going to know about what is Euclidean algorithm which is used to find Gcd of two numbers and how we can apply this concept in our programs.
BruteForce approach to find Gcd
If , we have to calculate the Gcd of two numbers a , b then the basic approach is to traverse form 1 to min(a,b) and then find max value of iteration variable which divide both numbers.
We have same approach in updated version also in which , we have to traverse only from 1 to Square root min(a,b). But both of two approach are Brute force approach and have complexicity of O(min(a,b)) and O(sqrt(min(a,b))) respectively.
Let see code in C++
int GCD(int a,int b)
{
int min_value=min(a,b);
int max_value=max(a,b);
int Gcd=1;
if(max_value%min_value==0) { Gcd=min_value; }
else
{
for(int i=1;i<=sqrt(min_value)+1;i++) {if(a%i==0 && b%i==0) Gcd=i;}
}
return Gcd;
}
This approach is quit fine for small values but for bigger values (in millions) this approach fail and may give some runtime errors. So try to ignore this approach and move forward for better approach named Euclidean algorithm.
Euclidean algorithm to find GCD
This approach asks you to perform successive division, first of the smaller of the
two numbers into the larger, followed by the resulting remainder divided into
the divisor of each division until the remainder is equal to zero. At that point,
look at the remainder of the previous division and that will be the GCD which you need.
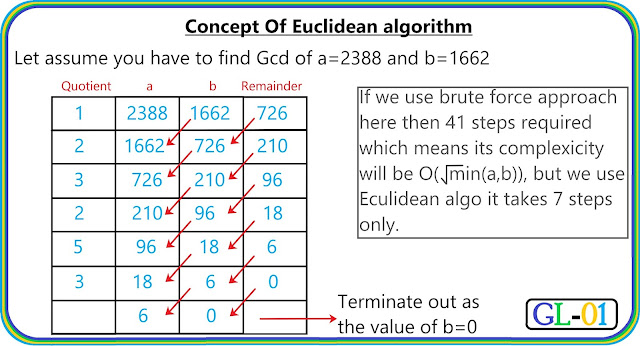
*If we subtract a smaller number from a larger (to reduce a larger number), Gcd doesn’t change. So if we keep subtracting repeatedly the larger of two, we end up with Gcd.
*Now instead of subtraction, if we divide the smaller number, the algorithm stops when we find remainder 0 then the ending number be the Gcd.
How to code Euclidean algorithm
In code we just two conditions for finding gcd(a , b):-
gcd(a,b)=agcd(b,amodb) ,if b=0,otherwise.
Let see code in C++(Recursive approach):-
int gcd (int a, int b)
{
if (b==0)
return a;
else
return gcd (b,a%b);
}
Time complexicity of Euclidean GCD
Basically it is simply algorithm based on recursive leap of faith, and the solution of this algo have surprising relation between Fibonacci series. That Fibonacci numbers grow exponentially, we get that the Euclidean algorithm works in O(log(min(a,b))).
Least common multiple(LCM)
The bonus part LCM, if you calculate GCD/HCF then mathematically finding LCM is easy and can be achieved by using this equation-
lcm(a,b)=a⋅bgcd(a,b)
Let see code in C++:-
int GCD (int a, int b)
{
if (b == 0)
return a;
else
return gcd (b, a % b);
}
int LCM (int a, int b)
{
return (a*b)/GCD(a,b);
}
Note:- In c++ their an Euclidean predefine function in c++ STL , which is "__gcd(a,b)".
Let see code in C++():-
int LCM (int a, int b)
{
return (a*b)/__gcd(a,b);
}
Practice Problem
May these Information will be useful for you,
Have a Nice Day😀😀😀.


Comments
Post a Comment